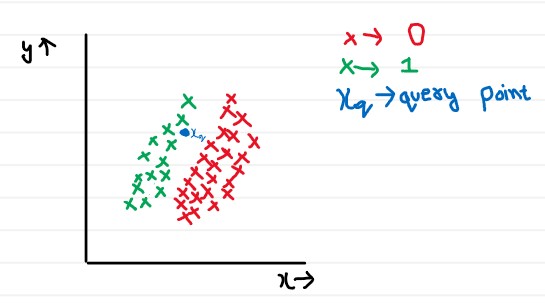
Hello world ! for Machine Learning
The iris dataset dataset contains
samples from the iris flower plant, classifying them into its different species based
on the following features:
(i) Sepal Length
(ii) Sepal Width
(iii) Petal Lenght
(iv) Petal Width
Before we connect mathematics and theory we need to learn some ML terminology.
Features:
The features in a ML problem are the attributes or properties which can have real values,
binary,
or String values sometimes. The below code snippet is from iris dataset :
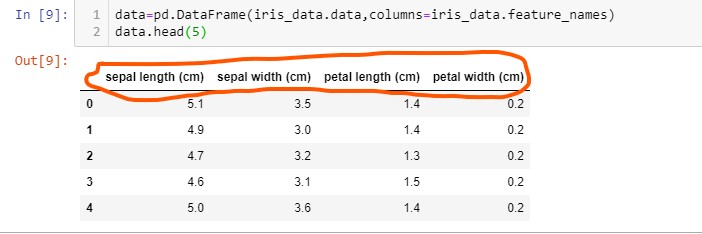
In this dataset all the features (sepal length ,sepal width , petal length and petal width )
have real values. Feature count in a dataset can vary from 1 to 100K depending upon the
problem
to be solved. We use feature values to construct a Machine Learning model from them and also
use
these values directly or indirectly as input to that model for results.
Target or Labels:
In datasets each row of different feature values corresponds to some class or a real value
which
we want to predict or analyse, this coulmn in a dataset can be called as target or label
column.
Particularly in most of the ML the problem is to predict value or a class from the given
value
of features.
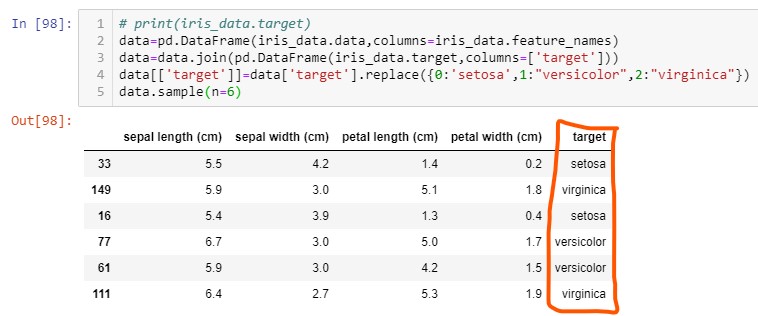
The above code snippet displays 6 random rows, note that each row has 'class' specified
under
the 'target' column as one of the three values from setosa, versicolor or veginica. We can
say
that in this dataset target values has three classes, but in some other dataset target
column
can also have real vaulues.
Classification and Regression
Many times ML is used to solve predictive problems. The predictive problems can be
classified
into two categories:
- Classification:
In these type of problems the target column contains the discrete values or different
classes. For example it could either be divided into binary like 0/1 or may be into
+ve and
-ve class. Iris dataset is an example of classification problem in which we have
class
lables (setosa, versicolor and virginica). Some more examples of classification
are:
$(i)$ Predicting if the given review about some product is negative or positive-
Target
column may contain +ve and -ve or may be 0 for negative and 1 for positive.
$(ii)$ Analysing the X-ray image of tumor and predicting if tumor is cancerous or
not-
Target column may contain 0 or 1 values.
$(iii)$ Predicting if the given email can be categorized into spam or not- Target
column may
contain 0/1 or "spam"/"not spam" values
- Regression:
In these type of predictive problems unlike classification, target column contains
continous
values. Most of the times in regression problems target values are real values.
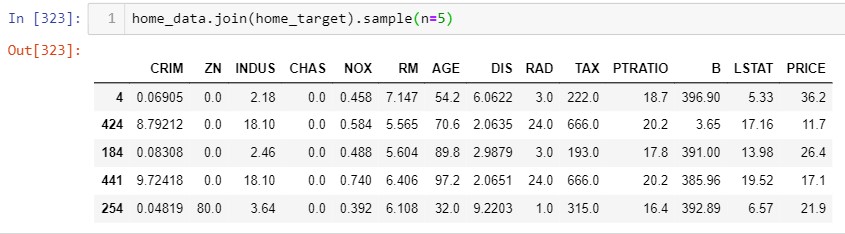
The above snippet is from famous Boston house-price dataset, note that "Price"
column being
target column contains the prices of house based on the features from various
aspects. In
the target column we have real values as the median price of owner occupied homes in
\$1000s. Some more examples of regression problems are:
$(i)$ Predicting the price of a stock.
$(ii)$ Predicting the release year of a song from audio features
$(iii)$ Predicting the student performance in secondary education (high school).
Machine Learning Model:
A ML model can be described as any sequence of functions which take features as an Input and
generates some prediction from them. For instance if we are given a task of predicting the
class
of iris flowers from a given set of 'features' then we need to make a model for this
problem.
Lets assume that we analysed the dataset and found the following inferences:
$1.$ $99.5$% of flowers which have 'sepal length' below $5.6 cm$ are 'setosa'.
$2.$ $93$% of flowers which have 'sepal width' less than $3.0 cm$ are either 'versicolor' or
'virginica'.
Now as we have above inference, a simple ML model could be like :
if sepal_length > 5.6:
return 'versicolor or virginica'
else:
return 'setosa'
The above code is just an intuition of ML model, in real world problems making an ML model
is
not that simple.
As we know some basics of ML termiology we can start connecting dots between Mathematics and
Data.